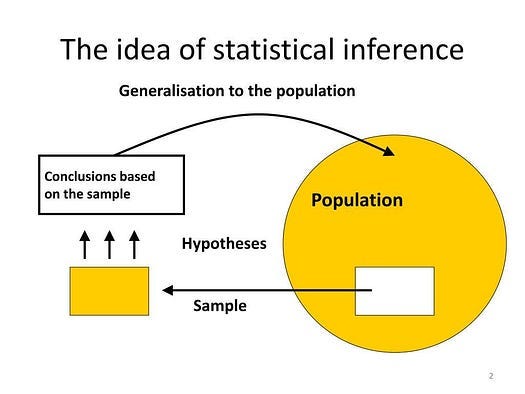
The Idea of Statistical Inference: Making Sense of Numbers.

The complete game of Stats is to make a guess on Sample and make Predictions or Inferences about Population.

Population & Sample

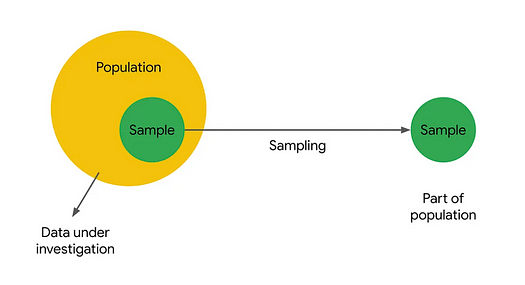
Its all about choosing the unbiased or best sample or small slice or chunk from population which best describes or the best representative of my whole population.

Population : The Population is the Entire group that we are taking for analysis or prediction.

For instance, a population might be the set of:

All students at a university
All the cell phones ever manufactured by a company
All the forests on Earth

Sample : Sample is the Subset of the Population (i.e. Taking random samples from the population). The size of the sample is always less than the total size of the population.

A sample is a subset of a population.

Samples drawn from the above populations might be:

The math majors at the university
The cell phones manufactured by the company in the last week
The forests in Canada

Data professionals use samples to make inferences about populations. In other words, they use the data they collect from a small part of the population to draw conclusions about the population as a whole.

or may be..

Hakuna Matata Time:-

Let’s breakdown in simpler terms:-

Now, assume you are cooking a meal for your party and we all as humans taste the meal before we serve to our guests.

Agree so far..

Although I never do because I am not good in cooking at all. 😂

Scenario:

Imagine you are preparing a large pot of soup for a dinner party. Before serving, you taste a spoonful of the soup to determine if it is salty or tasty, we then assume that the entire pot of soup is salty or tasty based on that small sample.

That’s the key Idea of one point estimate or Inferential Statsitics

Step-by-Step Process:

1.Define the Population and Sample:

Population: The entire pot of soup.
Sample: The spoonful of soup you tasted.

2. Collect Data:

You taste a spoonful of soup and assess its flavor.

3. Assumption and Inference:

Based on the taste of the spoonful (sample), you make an inference about the taste of the entire pot of soup (population).Assuming the entire pot has a similar taste based on the sample.

4. Inferential Statistics in Action:

Sample Mean (x̄): The taste quality you experience from the spoonful. Let’s say you rate it as “tasty.”
Population Mean (μ): The inferred taste quality of the entire pot of soup. You assume it is also “tasty” based on your sample.

Importance of Inferential Statistics in Cooking:

Practicality:

It is impractical to taste the entire pot of soup. Tasting a small sample is a practical way to make a reasonable assumption about the whole dish.

Efficiency:

Tasting just a spoonful saves time and ensures the dish remains intact for serving.

Decision Making:

Based on the taste of the sample, you decide whether any adjustments are needed, such as adding more salt or seasoning.

Summary:

This method is practical and efficient, allowing you to make informed decisions about the dish without having to taste the whole pot. It demonstrates how inferential statistics can be applied to everyday tasks, helping in decision-making processes based on samples rather than the entire population.

WAIT,

How will you decide that, the spoon you took from complete bowl is a best representative of your dish. May be you took a sample from the middle of bowl where salt content is less or may be you tasted from side of the bowls where salt content is still not well cooked.

Your Guess can be biased.